شار مغناطیسی
مطابق با شکل زیر میدانی مغناطیسی و یکنواخت را در نظر بگیرید که از صفحهای عبور میکند.
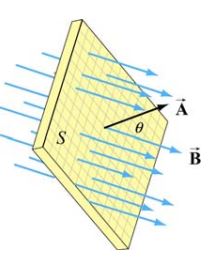
بردار سطح بهصورت
در نظر گرفته میشود. در این فرض A برابر با اندازه سطحی است که میدان مغناطیسی از آن عبور میکند؛ همچنین
بردار عمود به سطح را نشان میدهد که به سمت بیرون در نظر گرفته میشود. با توجه به این فرضیات، شار گذرنده از سطح، برابر است با:

در رابطه بالا θ، زاویه بین بردارهای
و را نشان میدهد. در حالتی که میدان یکنواخت نباشد، شار مغناطیسیِ
برابر است با:
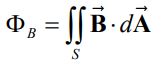
واحد شار مغناطیسی در سیستم SI را «وِبِر» مینامند که با Wb نشان داده میشود. ۱ وبر برابر است با:
![]()
با توجه به تعریف شار مغناطیسی، قانون القای فارادی را میتوان به صورت زیر توصیف کرد:
نیروی محرکه (ε) ایجاد شده در یک حلقه برابر با منفی تغییرات شار مغناطیسی است که از سطح سیمپیچ عبور میکند. بنابراین نیرو محرکه ایجاد شده برابر است با:
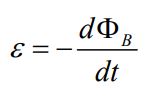
برای سیمپیچی که از N حلقه تشکیل شده، نیروی محرکه القا شده برابر است با:

با ترکیب روابط ۱ و ۲، نیرو محرکه القا شده را میتوان تابعی از تغییرات سطح و زاویه، به شکل زیر بدست آورد.
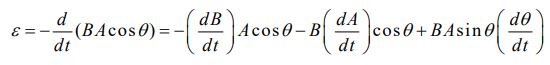
در نتیجه، نیروی محرکه القا شده در یک حلقه تحت شرایط زیر بوجود میآید.
- تغییر میدان مغناطیسی
- با زمان (شکل زیر)

- تغییر مساحتِ قرار گرفته در معرض میدان مغناطیسی (شکل زیر)
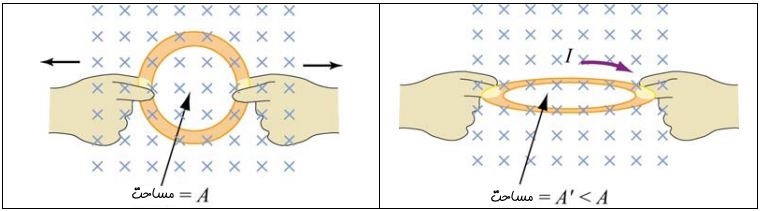
- تغییر زاویه بین
- و
- با زمان (شکل زیر)

قانون لنز (Lenz Law)
جهت جریان ایجاد شده در سیم را با استفاده از قانون لنز تعیین میکنند. این قانون بیان میکند که جریان القا شده در رسانا، میدانی تولید میکند که خلاف جهت تغییرات شار مغناطیسی عمل میکند. بهمنظور توضیح قانون لنز، مطابق با شکل زیر حلقهای را در نظر بگیرید که در میدانی مغناطیسی قرار گرفته.

شکل ۱ بهمنظور تعیین جهت جریان القا شده به ترتیب زیر عمل کنید:
- جهت مثبتی برای بردار
- با زمان (شکل زیر)
- در نظر بگیرید.
- با فرض اینکه میدانِ
- متقارن باشد، حاصلضرب داخلی دو بردار و
- را بیابید.
- با مشتقگیری از شار بدست آمده در مرحله قبل، نرخ تغییرات آن را نسبت به زمان (
- ) بدست آورید. سه حالت زیر وجود خواهد داشت:

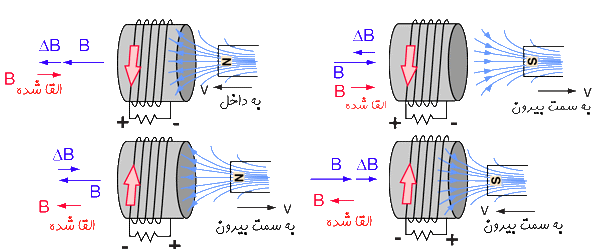
در مرحله آخر با استفاده از قانون دست راست، جهت جریان القاء شده بدست میآید. انگشت شست خود را در جهت بردار A بگیرید؛ در این حالت اگر ۰<ε، جهت انگشتان بسته شما، جهت جریان و اگر ۰>ε باشد، جهت جریان القا شده، خلاف جهت انگشتان بسته شما است. با استفاده از ۴ مرحله بالا میتوانید جهت جریان ایجاد شده در حلقه قرار گرفته در میدان مغناطیسی را بدست آورید. شکل زیر ۴ حالت متفاوت از جریان القا شده در میدان مغناطیسی متغیر را نشان میدهد.
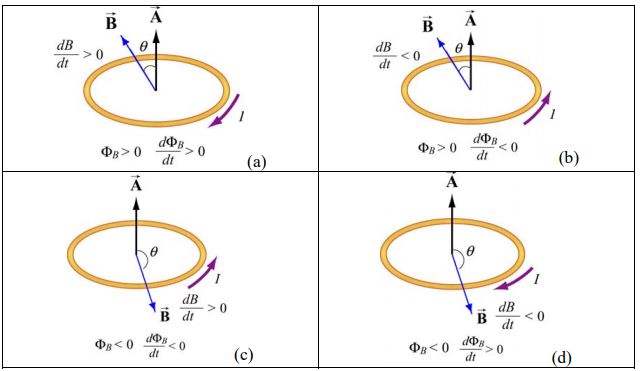
حالات بالا به طور خلاصه در جدول زیر بیان شدهاند.
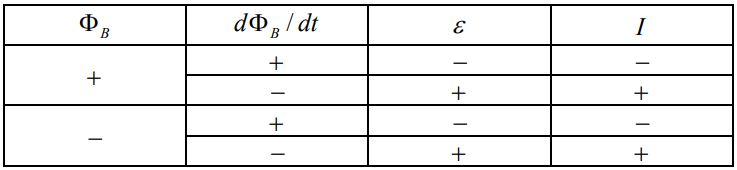
توجه داشته باشید که علامت منفی و مثبتِ جریانِ I، به ترتیب معادل با ساعتگرد و پادساعتگرد بودن جریان الکتریکی است. جهت بررسی نحوه عملکرد قانون لنز، مطابق شکل زیر حلقهای را تصور کنید که آهنربایی از سمت قطب شمالش به آن نزدیک میشود.
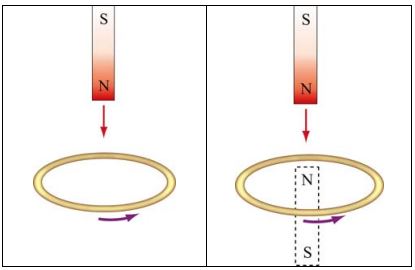
قبلا نیز ذکر کردیم که جهت میدان مغناطیسی یک آهنربا از قطب شمال به قطب جنوبش است. با توجه به اینکه جهت بردار A به سمت بالا و B به سمت پایین است، در نتیجه شارِ
منفی است. در حالی که آهنربا به سمت حلقه در حال نزدیک شدن است، میدان مغناطیسی عبوری از حلقه نیز با زمان افزایش مییابد () که منجر به عبور شار بیشتر با زمان میشود. در نتیجه تغییرات شار عبوری از حقله برابر با
است. از این رو با توجه به رابطه القای فارادی، نیرو محرکه القا شده مثبت خواهد بود (ε>0). حال با استفاده از قانون دست راست و اینکه نیرو محرکه بدست آمده مثبت است، جهت جریان القا شده در این حالت، به صورت پادساعتگرد خواهد بود.
شکل زیر قانون لنز را به طور خلاصه نشان میدهد.
نیروی محرکه ایجاد شده در نتیجه حرکت
همانطور که در تصویر زیر نشان داده شده، میلهای رسانا را به طول L تصور کنید که در میدانی مغناطیسی در حال حرکت میباشد. جهت این میدان به سمت درون صفحه است.
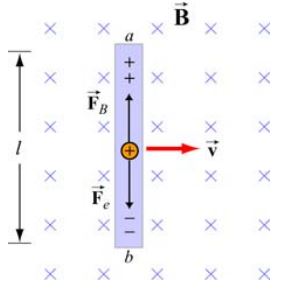
در مطلب مقدمه میدان مغناطیسی عنوان کردیم که به ذره باردار در حال حرکت در میدان مغناطیسی، نیرویی برابر با
وارد میشود. در این مورد نیز به ذرات مثبت نیرویی به سمت بالا وارد خواهد شد؛ در نتیجه به نظر میرسد میله به دو بخش با ذرات باردار مثبت و منفی تبدیل میشود.
با قرار گرفتن بارهای مثبت و منفی در دو سر میله، میدانی الکتریکی (
) بین آنها بوجود خواهد آمد که منجر به وارد شدن نیرویی برعکس نیروی مغناطیسی به بارها میشود [
]. در حالت تعادل، بارها جابجایی خالصی را در میله تجربه نمیکنند؛ در نتیجه نیروی ناشی از میدان مغناطیسی (qvB) و میدان الکتریکی (Eq) با یکدیگر برابر خواهند شد. از این رو با برابر قرار دادن آنها داریم:
![]()
در نتیجه اختلاف پتانسیل ایجاده شده در دو سمت رسانای مفروض، برابر است با:
![]()
از آنجایی که اختلاف پتانسیل شرح داده شده در نتیجه حرکت رسانا است، بنابراین آن را اختلاف پتانسیل حرکتی مینامند. در حالت کلی اختلاف پتانسیل حرکتی ایجاد شده در یک مسیر بسته را میتوان مطابق با رابطه زیر توصیف کرد.
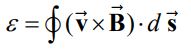
در رابطه بالا
دیفرانسیلِ بردار طول را نشان میدهد. حال تصور کنید که میله رسانایی بخشی از یک مدار را مطابق با شکل زیر تشکیل میدهد. توجه داشته باشید که میدان مغناطیسی به درون صفحه در نظر گرفته شده و R مقاومت مدار است.
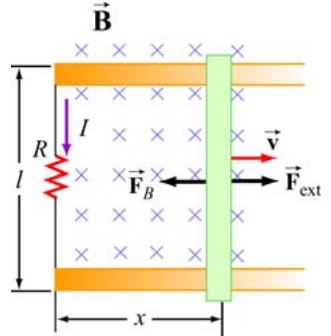
فرض کنید نیروی ثابت Fext به میله متحرک وارد شود. در نتیجه میله مذکور با سرعت ثابت v به سمت راست حرکت خواهد کرد. از آنجایی که مساحت حلقه متغیر است، بنابراین شار بدست آمده در هر لحظه برابر است با:
![]()
در نتیجه باتوجه به قانون القای فارادی، نیرو محرکه القا شده برابر با مقدار زیر بدست میآید.
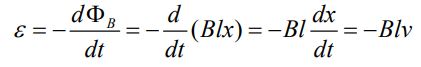
در رابطه بالا dx/dt=v برابر با سرعت میله است؛ جریان القا شده در این مدار را میتوان مطابق با رابطه زیر بدست آورد.
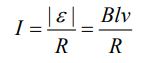
برای مشاهده ویدیو آموزشی این قسمت کلیک کنید.
منبع: فرادرس