میدان مغناطیسی سیم حامل جریان الکتریکی

قانون اورستد

در سال 1800 الساندرو ولتا باتری ولتایی که اولین باتری الکتریکی بود را اختراع کرد. این باتری ابتدایی متشکل از چندین دیسک فلزی بود که هر کدام از آن‌ها از فلزی غیر مشابه تشکیل شده و در یک سری متناوب قرار می‌گرفتند و توسط نوار لنت‌های مرطوب با الکترولیت از هم جدا می‌شدند.

سال بعد اورستد شروع به تحقیق درباره ماهیت الکتریسیته و انجام اولین آزمایش‌های الکتریکی خود کرد. در سال 1820 هنگامی که او در حال انجام آزمایش در کلاس برای دانشجویانش بود جریان الکتریکی را از یک سیم عبور داد و متوجه شد که سوزن قطب نمای مغناطیسی حرکت می‌کند.

این رویداد به وضوح نشان‌دهنده رابطه‌ای بین مغناطیس و الکتریسیته بود و باعث شد اورستد اولین کسی باشد که نیروی الکترومغناطیس را شناسایی می‌کند. مشاهده وی در ژوئیه 1820 در جزوه ای تحت عنوان «آزمایشاتی در مورد تأثیر جریان الکتریکی بر عقربه مغناطیسی» منتشر شد. با آزمایش‌های بیشتر اورستد دریافت که جریان الکتریکی در یک سیم یک اثر مغناطیسی دایره‌ای در اطراف خود ایجاد می‌کند.

تصویر ۱: فیزیکدان دانمارکی که متوجه شد در عبور جریان الکتریکی از یک سیم، عقربه مغناطیسی نیز حرکت می‌کند.

برای آشنایی بیشتر با ویژگی‌های میدان مغناطیسی، می‌توانید فیلم آموزش فیزیک پایه یازدهم را که توسط فرادرس ارائه شده است مشاهده کنید. لینک این آموزش در ادامه آورده شده است.

• برای دیدن فیلم آموزش فیزیک پایه یازدهم + اینجا کلیک کنید.

میدان مغناطیسی حاصل از جریان الکتریکی

هانس کریستین اورستد فیزیکدان دانمارکی (1851-1777) رابطه ریاضی حاکم بر قدرت یک سیم حامل جریان را کشف کرد که اکنون به آن قانون اورستد گفته می‌شود. کشف اورستد اولین ارتباط بین الکتریسیته و مغناطیس بود و اولین قانونی بود که این دو ماهیت فیزیکی را به یکدیگر مرتبط می‌کرد. قانون دیگری که به ارتباط بین الکتریسیته و مغناطیس می‌پردازد، قانون فارادی است.

این دو قانون یعنی قانون اورستد و قانون فارادی بخشی از معادلات حاکم بر الکترومغناطیس یعنی معادلات ماکسول را تشکیل می‌دهند. اورستد دریافت برای یک سیم که از آن جریان مستقیم عبور می‌کند ویژگی‌های زیر برقرار است:

• خطوط میدان مغناطیسی سیم حامل جریان را احاطه می‌کنند.
• خطوط میدان مغناطیسی در یک صفحه عمود بر سیم قرار دارند.
• اگر جهت جریان معکوس شود جهت میدان مغناطیسی نیز معکوس می‌شود.
• قدرت میدان مستقیماً با بزرگی جریان متناسب است.
• مقاومت میدان در هر نقطه با فاصله از سیم رابطه عکس دارد.

کشف مفهوم الکترومغناطیس توسط اورستد مجموعه‌ای از مفاهیم جدید را به وجود آورد که بنیان دنیای مدرن مجهز به فناوری را بنا نهاد.

اندکی پس از کشف اورستد فیزیکدان فرانسوی «آندره ماری آمپر» (Andre-Marie Ampere) رابطه ریاضی را برای نمایش نیروهای مغناطیسی موجود بین رساناهای حامل جریان بیان کرد. پس از ۴۰ سال دانشمند اسکاتلندی «جیمز کلارک مکسول» (James Clerk Maxwell) این معادله را به گونه‌ای اصلاح کرد تا بتوان از آن در شرایطی که جریان ثابت نیست نیز استفاده کرد و این معادله یکی از چهار معادله معروف وی شد که ثابت می‌کند نور یک موج الکترومغناطیس است.

الکترومغناطیس اساس بسیاری از دستگاه‌ها از جمله موتور الکتریکی، میکروفون، ژنراتور الکتریکی، بلندگو و ترانسفورماتورها است.

بیان ریاضی میدان مغناطیسی حاصل از جریان الکتریکی در یک سیم راست

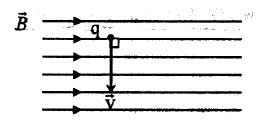
میدان‌های مغناطیسی مانند میدان الکتریکی از بار به وجود می‌آیند اما نوع این بارها متفاوت است. سیم مستقیم بلند حامل جریان ساده‌ترین نمونه بار الکتریکی متحرک است که یک میدان مغناطیسی تولید می‌کند. می‌دانیم جهت نیرویی که یک بار در هنگام حرکت از طریق یک میدان مغناطیسی تجربه می‌کند از طریق قانون دست راست محاسبه می‌شود. در مورد سیم مستقیم بلند که جریان II را حمل می‌کند خطوط میدان مغناطیسی دور سیم قرار می‌گیرند. با قرار دادن انگشت شست دست راست در امتداد جهت جریان می‌توان با خم شدن انگشتان به دور سیم جهت میدان مغناطیسی را پیدا کرد.

تصویر ۲: پیدا کردن جهت میدان مغناطیسی در یک سیم حامل جریان

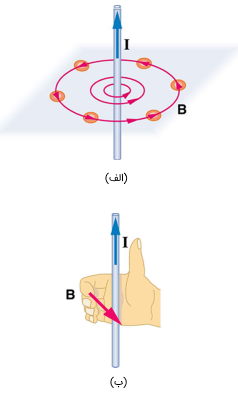
قدرت میدان مغناطیسی به جریان II در سیم و rr فاصله از سیم بستگی دارد.

B=μ0 I2π rμ0=4π×10−7 (TmsC)B=μ0 I2π rμ0=4π×10−7 (TmsC)

μ0μ0 ثابت تراوایی مغناطیسی است. دلیل این که به نظر نمی‌رسد μ0μ0 یک ثابت دلخواه باشد این است که واحدهای بار و جریان یعنی کولن و آمپر، برای دادن یک فرم ساده برای این ثابت انتخاب شده‌اند. همچنین می‌توان نشان داد که حاصلضرب μ0μ0 و ϵ0ϵ0 برابر با سرعت نور است و داریم:

c=1√ϵ0 μ0c=1ϵ0 μ0

اگر رابطه میدان الکتریکی یک سیم باردار یکنواخت را به خاطر آورید متوجه می‌شوید که این کمیت نیز با عامل 1r1r کاهش می‌یابد.

هیچ رابطه‌ای شبیه به قانون کولن که برای نیروی میدان الکتریکی بین دو ذره باردار برقرار است برای حالت مغناطیسی وجود ندارد زیرا میدان مغناطیسی برای یک بار نقطه‌ای مسئله‌ای پیچیده است و طبق مطالعات صورت گرفته و شواهد به دست آمده یک بار نقطه‌ای نمی‌تواند میدان مغناطیسی تولید کند.

تصویر ۳: میدان مغناطیسی اطراف یک سیم بلند حامل جریان

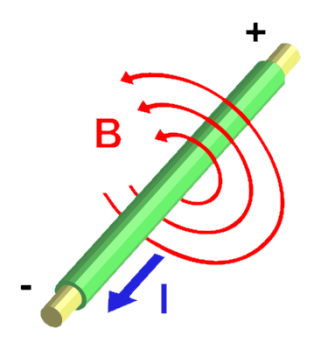
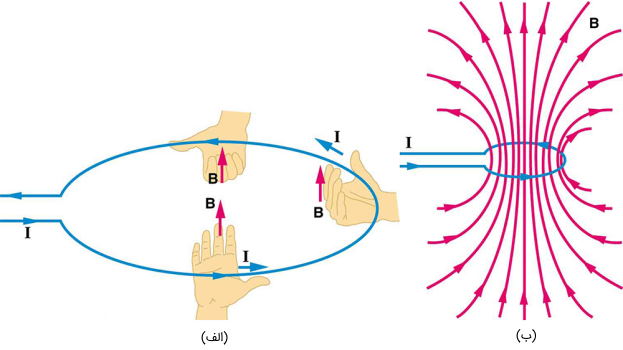
بیان ریاضی میدان مغناطیسی حاصل از جریان الکتریکی در یک سیم به صورت حلقه

اگر سیم صاف حاوی جریان را به صورت یک حلقه سیم حامل جریان درآوریم، رابطه ریاضی میان میدان و جریان به صورت زیر به دست می‌آید:

B=μ0I2RB=μ0I2R

که در این رابطه RR شعاع حلقه سیم حامل جریان است. این معادله بسیار شبیه معادله سیم راست است اما در مرکز حلقه دایره‌ای سیم قابل استفاده است. شباهت معادلات نشان می‌دهد که در مرکز یک حلقه می‌توان میدان مغناطیسی هم‌اندازه با یک سیم حامل جریان بدست آورد. یک راه برای بدست آوردن یک میدان مغناطیسی بزرگتر داشتن N حلقه سیم است، در این حالت میدان مغناطیسی برابر است با:

B=Nμ0I2RB=Nμ0I2R

توجه داشته باشید که هرچه حلقه بزرگتر باشد میدان در مرکز آن کوچکتر است زیرا فاصله جریان تا مرکز حلقه بیشتر می‌شود.

تصویر ۴: میدان مغناطیسی یک حلقه سیم حامل جریان

بیان ریاضی میدان مغناطیسی حاصل از جریان الکتریکی در یک سلونوئید

سلونوئید یک سیم‌پیچ شامل تعداد زیادی حلقه جریان است.به دلیل ساختار سلونوئید میدان در داخل آن یکنواخت و قوی است. همچنین میدان در خارج سلونوئید تقریباً صفر است.

تصویر ۵: میدان مغناطیسی ناشی از یک سلونوئید حامل جریان

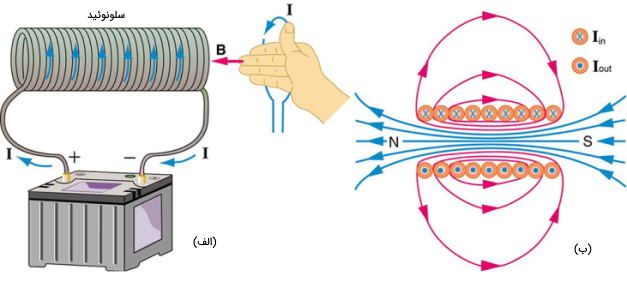
میدان مغناطیسی داخل یک سلونوئید حامل جریان از نظر جهت و اندازه بسیار یکنواخت است. با این حال میدان در نزدیکی لبه‌های ابتدایی و انتهایی آن شروع به تضعیف و تغییر جهت می‌کند. میدان خارج سلونوئید دارای پیچیدگی‌های مشابه حلقه‌های تخت و آهن‌ربا است اما قدرت میدان مغناطیسی درون یک سلونوئید به سادگی توسط رابطه زیر بیان می‌شود:

B=μ0nIB=μ0nI

در رابطه بالا nn تعداد حلقه‌های سلونوئید در واحد طول است، یعنی داریم:

n=Nln=Nl

که NN تعداد حلقه‌ها و ll طول سیم است. توجه داشته باشید که BB مربوط به میدان در هر نقطه از منطقه یکنواخت داخلی است و فقط میدان مربوط به مرکز سلونوئید نیست.

مثال‌های مربوط به میدان مغناطیسی حاصل از جریان الکتریکی

مثال ۱: جریان الکتریکی را برای یک سیم بلند که یک میدان مغناطیسی دو برابر میدان مغناطیسی زمین در فاصله 55 سانتی‌متری از سیم تولید می‌کند را محاسبه کنید.

پاسخ: میدان مغناطیسی زمین در حدود 5×10−5T5×10−5T است. بنابراین میدان در فاصله ۵ سانتی‌متری از سیم برابر با 1×10−4T1×10−4T است. از آنجا که مقدار تمام دیگر کمیت‌ها مشخص است از معادله B=μ0I2πrB=μ0I2πr می‌توان برای محاسبه جریان استفاده کرد و داریم:

I=2πrBμ0=2π(5×10−2m)(1.0×10−4T)4π×10−7T⋅m/AI=2πrBμ0=2π(5×10−2m)(1.0×10−4T)4π×10−7T⋅m/A
⇒I=25 (A)⇒I=25 (A)

مثال ۲: میدان درون یک سلونوئید 22 متری که 20002000 حلقه دارد و جریان 16001600 آمپری حمل می‌کند چه قدر است؟

پاسخ: برای یافتن میدان درون یک سلونوئید از رابطه B=μ0nIB=μ0nI استفاده می‌کنیم. بدین منظور با توجه به صورت سوال می‌دانیم طول سلونوئید ۲ متر است و ۲۰۰۰ حلقه دارد. بدین ترتیب داریم:

n=20002=1000 m−1n=20002=1000 m−1

بدین ترتیب با استفاده از رابطه میدان در سلونوئید داریم:

B=μ0nI=(4π ×10−7 T.mA)(1000 m−1)(1600 A)B=μ0nI=(4π ×10−7 T.mA)(1000 m−1)(1600 A)
⇒B=2.01 T⇒B=2.01 T

نتیجه به دست آمده یک میدان مغناطیسی بزرگ است که می‌تواند از طریق یک سلونوئید با قطر بزرگ ایجاد شود، مانند موارد استفاده پزشکی از تصویربرداری تشدید مغناطیسی یا همانMRI. جریان بسیار زیاد نشان می‌دهد که این قدرت برای میدان مغناطیسی به راحتی به دست نمی‌آید. چنین جریان بزرگی از طریق 1000 حلقه که به طول یک متر فشرده شده‌اند باعث گرمای زیاد سلونوئید می‌شود. با استفاده از سیم‌های ابررسانا می‌توان جریان‌های بزرگتری نیز به دست آورد هرچند هزینه آن گران می‌شود. در هر صورت برای مواد ابررسانا نیز یک حد بالا برای جریان وجود دارد زیرا حالت ابررسانا توسط میدان‌های مغناطیسی بسیار بزرگ مختل می‌شود.

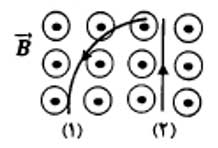
مثال ۳: سه سیم در گوشه‌های یک مربع قرار دارند که جریان همه آن‌ها 2 آمپر است، این موضوع در شکل زیر نیز نمایش داده شده است. اگر طول هر ضلع مربع 1 سانتی‌متر باشد مقدار میدان مغناطیسی گوشه دیگر مربع یعنی نقطه P را محاسبه کنید.

تصویر ۶: میدان مغناطیسی حاصل از جریان الکتریکی سه سیم حامل جریان در نقطه PP

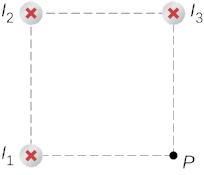
پاسخ: میدان مغناطیسی ناشی از هر سیم در نقطه مورد نظر قابل محاسبه است. فاصله مورب با استفاده از قضیه فیثاغورث محاسبه می‌شود. سپس جهت سهم هر سیم در نقطه مورد نظر رسم می‌شود. توجه کنید که بردارهای رسم شده در نقطه P مماس بر منحنی میدان هستند. در نهایت با استفاده از جبر برداری میدان در نقطه P محاسبه می‌شود.

سیم‌های 1 و 3 هر دو دارای میدان مغناطیسی برابر در نقطه P هستند و داریم:

B1=B3=μ0I2πR=(4π×10−7T⋅m/A)(2A)2π(0.01m)=4×10−5TB1=B3=μ0I2πR=(4π×10−7T⋅m/A)(2A)2π(0.01m)=4×10−5T

سیم 2 فاصله طولانی‌تر تا نقطه P دارد و سهم میدان مغناطیسی آن برابر است با:

B2=μ0I2πR=(4π×10−7T⋅m/A)(2A)2π(0.01414m)=3×10−5TB2=μ0I2πR=(4π×10−7T⋅m/A)(2A)2π(0.01414m)=3×10−5T

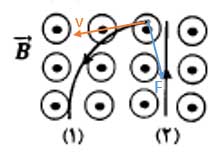
بردارهای مربوط به هر یک از میدان‌های مغناطیسی در نقطه P در شکل زیر نشان داده شده‌اند.

تصویر ۷: میدان مغناطیسی حاصل از جریان الکتریکی سه سیم در نقطه PP

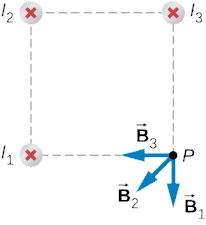
میدان مغناطیسی در نقطه P و در راستای x حاصل از سیم 3 و مولفه x سیم 2 است. بدین ترتیب میدان مغناطیسی در راستای x برابر است با:

Bnetx=−4×10−5T–2.83×10−5Tcos(45o)=−6×10−5TBnetx=−4×10−5T–2.83×10−5Tcos⁡(45o)=−6×10−5T

همچنین مولفه y میدان مغناطیسی در نقطه Pبه صورت زیر محاسبه می‌شود:

Bnety=−4×10−5T–2.83×10−5Tsin(45o)=−6×10−5TBnety=−4×10−5T–2.83×10−5Tsin⁡(45o)=−6×10−5T

بنابراین میدان مغناطیسی خالص حاصل از این دو جزء برابر است با:

Bnet=√B2netx+Bnety=√(−6×10−5T)2+(−6×10−5T)2=8.48×10−5T.Bnet=Bnetx2+Bnety=(−6×10−5T)2+(−6×10−5T)2=8.48×10−5T.

هندسه این مسئله منجر به ایجاد یک میدان مغناطیسی در جهت −x−x و yy می‌شود. اگر جریان‌ها مقادیر متفاوتی داشته باشند یا سیم‌ها در موقعیت‌های مختلفی قرار داشته باشند مقادیر میدان در راستای xx و yy متفاوت خواهد بود. صرف نظر از نتایج عددی کار بر روی مولفه‌های بردار سبب ایجاد میدان مغناطیسی در نقطه مورد نیاز می‌شود.

hkvCd ohck

وقتی صفحه های خازن دارای بار الکتریکی می شوند در خازن انرژی ذخیره می شود. برای اینکه انرژی خازن را مشاهده کنیم، کافی است دو سر یک خازن پر شده را به دو سر یک لامپ کوچک وصل کنیم. به شرط آنکه ظرفیت و اختلاف پتانسیل خازن به اندازه کافی زیاد باشد، لامپ برای مدتی روشن و سپس خاموش می شود.

اثبات فرمول محاسبه انرژی خازن

در حین شارژ شدن خازن باتری کار W=QΔV را روی بار انجام می دهد. و با توجه به افزایش اختلاف پتانسیل دو صفحه در حین شارژ شدن، به ازای انتقال هر بار باید کار بیشتری انجام شود.

و از آنجایی که در این فرایند ظرفیت خازن همواره ثابت می ماند و طبق رابطه V=Q/C ، اختلاف پتانسیل تابع خطی از بار Q است. بنابراین می توان مقدار متوسط اختلاف پتانسیل را به صورت زیر بدست آورد.

کار انجام شده برای باردار شدن کامل خازن برابر با حاصل ضرب کل بارهای جزئی منتقل شده (Q) در اختلاف پتانسیل متوسط است. یعنی :

این کار به صورت انرژی پتانسیل الکتریکی در میدان الکتریکی فضای بین صفحه های خازن ذخیره می شود.

که در این رابطه U بر حسب ژول (J) و Q بر حسب کولن (c) و V بر حسب ولت (V) و C بر حسب فاراد (F) است.

مثال : خازن C=5µF را با پتانسیل V=60V شارژ و آن را از مدار جدا می سازیم.

الف) بار و انرژی ذخیره شده در خازن را بدست آورید.

ب) اگر سطح اشتراک صفحات را دو برابر و فاصله آن ها را نصف کنیم، آنگاه  ظرفیت و بارالکتریکی و اختلاف پتانسیل الکتریکی و انرژی ذخیره شده در خازن چه تغییری می کند؟

حل مثال :

تمرین ها

تمرین ۱: خازن تختی را پس از پر کردن از باتری جدا می کنیم، اگر در این حالت یک دی الکتریک بین دو صفحه ی آن قرار دهیم به ترتیب انرژی و اختلاف پتانسیل دو سر آن چگونه تغییر می کند؟

تمرین ۲: با تخلیه‌ی قسمتی از بار الکتریکی یک خازن پر شده، اختلاف پتانسیل دو سر آن ۸۰ درصد کاهش می‌یابد. انرژی این خازن چند درصد کاهش می‌یابد؟

تمرین ۳: ظرفیت خازنی ۱۲ میکروفاراد و بار الکتریکی آن q است. اگر ۳ میلی کولن بار مثبت را از صفحه منفی جدا کرده و به صفحه مثبت منتقل کنیم، انرژی ذخیره شده در خازن به اندازه ۸ ژول افزایش می یابد. Q را محاسبه کنید.

---

ویدیو آموزشی 

به ویدیو آموزشی که توسط استاد مصطفی کبیری آماده شده است، توجه کنید.

 

---

امتحان القای الکترومغناطیسی فیزیک یازدهم

برای آشنایی کاربران عزیز سایت آموزشی فیزیکفا، نمونه سوال امتحانی از فیزیک یازدهم ( فصل چهارم رشته ریاضی و نیمه دوم فصل سوم رشته تجربی : القای الکترومغناطیسی) آماده شده است تا با سوالات استاندارد این پایه آشنایی بیشتری پیدا کنند.توصیه می شود ابتدا سعی کنید سوالات را بر اساس دانش خود از این فصل حل کنید. سپس پاسخ ما را دانلود کرده و با پاسخ خود مقایسه کنید تا به نقاط ضعف خود در این مبحث دست یابید و در رفع آن برآیید. سوالات طرح شده بر اساس کتاب درسی فیزیک یازدهم بوده و اگر مطالب کتاب را خوب بلد باشید، باید به همه سوالات پاسخ صحیح دهید. برای تسط بیشتر شما به مباحث کتاب درسی جزوه هایی در سایت از این فصل کتاب فیزیک یازدهم قرار گرفته است که می توانید از طریق لینک های زیر به آنها دسترسی پیدا کنید.

پدیده القای الکترومغناطیسی

قانون القای الکترومغناطیسی فاراده

قانون لنز

القاگرها

جریان متناوب

حل تمرین های فصل چهارم فیزیک یازدهم

 

دانلود نمونه سوال امتحانی القای الکترومغناطیسی طراحی شده توسط مصطفی کبیری:

دانلود نمونه سوال القای الکترومغناطیسی

 

برای دانلود پاسخ تشریحی نمونه سوال به لینک منبع مطلب رجوع کنید. فیزیکفا

قانون القای الکترومغناطیسی فاراده

شار مغناطیسی

مطابق با شکل زیر میدانی مغناطیسی و یکنواخت را در نظر بگیرید که از صفحه‌ای عبور می‌کند.

بردار سطح به‌صورت $$\overrightarrow{A}=A\hat{n}$$

در نظر گرفته می‌شود. در این فرض A برابر با اندازه سطحی است که میدان مغناطیسی از آن عبور می‌کند؛ هم‌چنین $$\hat{n}$$

بردار عمود به سطح را نشان می‌دهد که به سمت بیرون در نظر گرفته می‌شود. با توجه به این فرضیات، شار گذرنده از سطح، برابر است با:

رابطه ۱

در رابطه بالا θ، زاویه بین بردار‌های $$\hat{n}$$

و $$\overrightarrow{B}$$ را نشان می‌دهد. در حالتی که میدان یکنواخت نباشد، شار مغناطیسیِ $${\Phi }_B$$

برابر است با:

واحد شار مغناطیسی در سیستم SI را «وِبِر» می‌نامند که با Wb نشان داده می‌شود. ۱ وبر برابر است با:

با توجه به تعریف شار مغناطیسی، قانون القای فارادی را می‌توان به صورت زیر توصیف کرد:

نیروی محرکه (ε) ایجاد شده در یک حلقه برابر با منفی تغییرات شار مغناطیسی است که از سطح سیم‌پیچ عبور می‌کند. بنابراین نیرو محرکه ایجاد شده برابر است با:

رابطه ۲

برای سیم‌پیچی که از N حلقه تشکیل شده، نیروی محرکه القا شده برابر است با:

با ترکیب روابط ۱ و ۲، نیرو محرکه القا شده را می‌توان تابعی از تغییرات سطح و زاویه، به شکل زیر بدست آورد.

 

در نتیجه، نیروی محرکه القا شده در یک حلقه تحت شرایط زیر بوجود می‌آید.

1. تغییر میدان مغناطیسی $$\overrightarrow{B}$$

• با زمان (شکل زیر)
  
• تغییر مساحتِ‌ قرار گرفته در معرض میدان مغناطیسی (شکل زیر)
  
• تغییر زاویه بین $$\overrightarrow{B}$$
• و $$\overrightarrow{A}$$
  3. با زمان (شکل زیر)
     

  قانون لنز (Lenz Law)

  جهت جریان ایجاد شده در سیم را با استفاده از قانون لنز تعیین می‌کنند. این قانون بیان می‌کند که جریان القا شده در رسانا، میدانی تولید می‌کند که خلاف جهت تغییرات شار مغناطیسی عمل می‌کند. به‌منظور توضیح قانون لنز، مطابق با شکل زیر حلقه‌ای را در نظر بگیرید که در میدانی مغناطیسی قرار گرفته.

  

  شکل ۱

  به‌منظور تعیین جهت جریان القا شده به ترتیب زیر عمل کنید:

  1. جهت مثبتی برای بردار $$\overrightarrow{A}$$
• در نظر بگیرید.
• با فرض این‌که میدانِ $$\overrightarrow{B}$$
• متقارن باشد، حاصلضرب داخلی دو بردار $$\overrightarrow{A}$$ و $$\overrightarrow{B}$$
• را بیابید.
• با مشتق‌گیری از شار بدست آمده در مرحله قبل، نرخ تغییرات آن را نسبت به زمان ($$\frac{d{\Phi }_B}{dt}$$

3. ) بدست آورید. سه حالت زیر وجود خواهد داشت:
   

در مرحله آخر با استفاده از قانون دست راست، جهت جریان القاء شده بدست می‌آید. انگشت شست خود را در جهت بردار A بگیرید؛ در این حالت اگر ۰<ε، جهت انگشتان بسته شما، جهت جریان و اگر ۰>ε باشد، جهت جریان القا شده، خلاف جهت انگشتان بسته شما است. با استفاده از ۴ مرحله بالا می‌توانید جهت جریان ایجاد شده در حلقه قرار گرفته در میدان مغناطیسی را بدست آورید. شکل زیر ۴ حالت متفاوت از جریان القا شده در میدان مغناطیسی متغیر را نشان می‌دهد.

حالات بالا به طور خلاصه در جدول زیر بیان شده‌اند.

توجه داشته باشید که علامت منفی و مثبتِ جریانِ I، به ترتیب معادل با ساعتگرد و پادساعتگرد بودن جریان الکتریکی است. جهت بررسی نحوه عملکرد قانون لنز، مطابق شکل زیر حلقه‌ای را تصور کنید که آهنربایی از سمت قطب شمالش به آن نزدیک می‌شود.

قبلا نیز ذکر کردیم که جهت میدان مغناطیسی یک آهنربا از قطب شمال به قطب جنوبش است. با توجه به این‌که جهت بردار A به سمت بالا و B به سمت پایین است، در نتیجه شارِ $${\Phi }_B=-BA<0$$

منفی است. در حالی که آهنربا به سمت حلقه در حال نزدیک شدن است، میدان مغناطیسی عبوری از حلقه نیز با زمان افزایش می‌یابد ($$dB/dt>0$$) که منجر به عبور شار بیشتر با زمان می‌شود. در نتیجه تغییرات شار عبوری از حقله برابر با $$\frac{d{\Phi }_B}{dt}=-A\frac{dB}{dt}<0$$

است. از این رو با توجه به رابطه القای فارادی، نیرو محرکه القا شده مثبت خواهد بود (ε>0). حال با استفاده از قانون دست راست و این‌که نیرو محرکه بدست آمده مثبت است، جهت جریان القا شده در این حالت، به صورت پادساعتگرد خواهد بود.

شکل زیر قانون لنز را به طور خلاصه نشان می‌دهد.

قانون لنز در یک نگاه

نیروی محرکه ایجاد شده در نتیجه حرکت

همان‌طور که در تصویر زیر نشان داده شده، میله‌ای رسانا را به طول L تصور کنید که در میدانی مغناطیسی در حال حرکت می‌باشد. جهت این میدان به سمت درون صفحه است.

در مطلب مقدمه میدان مغناطیسی عنوان کردیم که به ذره باردار در حال حرکت در میدان مغناطیسی، نیرویی برابر با $${\overrightarrow{F}}_B=q\overrightarrow{v}\times \overrightarrow{B}$$

وارد می‌شود. در این مورد نیز به ذرات مثبت نیرویی به سمت بالا وارد خواهد شد؛ در نتیجه به نظر می‌رسد میله به دو بخش با ذرات باردار مثبت و منفی تبدیل می‌شود.

 

با قرار گرفتن بارهای مثبت و منفی در دو سر میله، میدانی الکتریکی ($$\overrightarrow{E}$$

) بین آن‌ها بوجود خواهد آمد که منجر به وارد شدن نیرویی برعکس نیروی مغناطیسی به بارها می‌شود [$${\overrightarrow{F}}_E=\overrightarrow{E}q$$

]. در حالت تعادل، بار‌ها جابجایی خالصی را در میله تجربه نمی‌کنند؛ در نتیجه نیروی ناشی از میدان مغناطیسی (qvB) و میدان الکتریکی (Eq) با یکدیگر برابر خواهند شد. از این رو با برابر قرار دادن آن‌ها داریم:

در نتیجه اختلاف پتانسیل ایجاده شده در دو سمت رسانای مفروض، برابر است با:

از آنجایی که اختلاف پتانسیل شرح داده شده در نتیجه حرکت رسانا است، بنابراین آن را اختلاف پتانسیل حرکتی می‌نامند. در حالت کلی اختلاف پتانسیل حرکتی ایجاد شده در یک مسیر بسته را می‌توان مطابق با رابطه زیر توصیف کرد.

در رابطه بالا $$d\overrightarrow{s}$$

دیفرانسیلِ بردار طول را نشان می‌دهد. حال تصور کنید که میله رسانایی بخشی از یک مدار را مطابق با شکل زیر تشکیل می‌دهد. توجه داشته باشید که میدان مغناطیسی به درون صفحه در نظر گرفته شده و R مقاومت مدار است.

فرض کنید نیروی ثابت F_ext به میله متحرک وارد شود. در نتیجه میله مذکور با سرعت ثابت v به سمت راست حرکت خواهد کرد. از آنجایی که مساحت حلقه متغیر است، بنابراین شار بدست آمده در هر لحظه برابر است با:

در نتیجه باتوجه به قانون القای فارادی، نیرو محرکه القا شده برابر با مقدار زیر بدست می‌آید.

در رابطه بالا dx/dt=v برابر با سرعت میله است؛ جریان القا شده در این مدار را می‌توان مطابق با رابطه زیر بدست آورد.

برای مشاهده ویدیو آموزشی این قسمت کلیک کنید.

 

منبع: فرادرس

نیروی مغناطیسی وارد بر ذره باردار متحرک در میدان مغناطیسی

در این آموزش به نیروی مغناطیسی وارد بر ذره باردار متحرک در میدان مغناطیسی می پردازیم.

آزمایش نشان می دهد که اگر ذره باردار q با سرعت v در میدان مغناطیسی B حرکت کند به شرطی که جهت حرکت ان با میدان مغناطیسی موازی نباشد، بر آن نیرویی وارد خواهد شد که بر راستای سرعت و میدان مغناطیسی عمود است. اندازه نیروی مغناطیسی وارد بر ذره باردار الکتریکی متحرک در میدان مغناطیسی از رابطه زیر بدست می آید :

که در این رابطه q بارالکتریکی ذره بر حسب C (کولن) و v اندازه سرعت ذره بر حسب m/s (متر بر ثانیه) و B اندازه میدان مغناطیسی بر حسب T (تسلا) و θ زاویه بین v و B بر حسب درجه است.

با توجه به مقدار سینوس در زاویه های صفر و ۱۸۰ درجه که برابر صفر می باشد، در صورتی که جهت حرکت ذره و راستای میدان موازی باشند، نیرویی به ذره باردار از طرف میدان مغناطیسی وارد نمی شود. و در صورتی که جهت سرعت ذره بر راستای میدان عمود باشد، نیروی مغناطیسی بیشینه می شود.

که می توان B را از رابطه زیر بدست آورد :

که از نظر یکایی، تسلا برابر می شود با :

چون یک آمپر برابر است با یک کولن بر ثانیه.

تسلا یکای بزرگی است و در برخی موارد از یکای قدیمی و کوچکتری به نام گاوس (با نماد G ) استفاده می کنیم به طوری که :

اندازه میدان مغناطیسی زمین در نزدیکی سطح زمین که در قطب ها مقدار بیشینه خود را دارد برابر (۰٫۶۵ G) و در استوا مقدار کمینه برابر (۰٫۲۵ G) است.

برای تعیین جهت نیروی مغناطیسی از قاعده دست راست استفاده می کنیم که در ویدیوی زیر می توانید این روش را بیاموزید:

 

مثال ۱: ذره ای با بار q=5µC با سرعت v در جهتی حرکت می کند که با میدان مغناطیسی یکنواخت به بزرگی ۰٫۰۴ تسلا زاویه ۳۰ درجه می سازد. اگر بزرگی نیروی مغناطیسی وارد بر این ذره برابر با ۴×۱۰^-۳ نیوتون باشد، بزرگی سرعت را محاسبه کنید.

حل مثال ۱:

مثال ۲: دو ذره هنگام عبور از میدان مغناطیسی برون سو، مسیرهایی مطابق شکل روبرو می پیمایند. درباره نوع بار هر ذره چه می توان گفت ؟

حل مثال ۲: جهت سرعت ذره خط مماس بر مسیر در نقطه شروع مسیر است . جهت انحراف ذره ، جهت نیروی وارد شده بر ذره است طوری که نیرو باید عمود بر سرعت باشد. مانند شکل زیر :

با توجه به نیروهای رسم شده در شکل و قاعدع دست راست ، میبینیم که از قاعدع دست راست پیروی نمی کند، بلکه با دست چپ می توان این بردارها را توجیه کرد بنابراین بار ذره ۱ منفی است.

برای ذره ۲ چون انحرافی در مسیر حرکت نمی بینیم، ذره بدون بار (خنثی) است.

مثال ۳: پروتونی با سرعت ۴×۱۰^۶ متر بر ثانیه مطابق شکل در میدان مغناطیسی یکنواختی به بزرگی ۲۰ میلی تسلا در حرکت است. بزرگی و جهت نیروی مغناطیسی وارد بر پروتون را تعیین کنید.

حل مثال ۳: جهت نیروی مغناطیسی با استفاده از قاعده دست راست، به سمت بیرون صفحه است.

مثال ۴:  یون مثبتی مطابق شکل روبرو به فضای بین صفحه های خازن مسطحی پرتاب می شود.

الف) جهت نیروی الکتریکی وارد بر این یون را رسم کنید.

ب) میدان مغناطیسی یکنواخت B باید در چه جهتی اثر کند تا نیروی مغناطیسی وارد بر یون بر خلاف جهت نیروی الکتریکی باشد؟

حل مثال ۴: الف) از فصل ۱ می دانیم که اگر بار مثبت باشد، نیروی الکتریکی و میدان الکتریکی هم جهت هستند و اگر بار منفی باشد، نیروی الکتریکی و میدان الکتریکی خلاف جهت هم هستند. میدان الکتریکی بین دو صفحه خازن از صفحه مثبت به سمت صفحه منفی است. بنابراین جهت نیروی الکتریکی هم جهت با آن و در جهت پایین است.

ب) نیروی مغناطیسی وارد بر یون مثبت باید خلاف جهت نیروی الکتریکی یعنی به سمت بالا باشد، که با توجه به جهت سرعت یون و قاعده دست راست، جهت میدان مغناطیسی به سمت داخل صفحه (درون سو) است.

می توانید ویدیو اموزشی این مبحث را به همراه مثال های بیشتر در مورد قاعده دست راست برای تعیین جهت مشاهده کنید.

 

قانون کولن

دید کلی

در اواخر قرن هیجدهم علوم تجربی به درجه‌ای از رشد و پیشرفت رسیده بود که بتوان مشاهدات دقیقی درباره نیروهای میان بارهای الکتریکی به عمل آورد. نتایج این مشاهدات را که در آن زمان فوق‌العاده مجادله‌آمیز بودند، نمی‌توان به این صورت بیان نمود. دو نوع و فقط دو نوع بار الکتریکی وجود دارد که ما اینها را به نام بارهای الکتریکی مثبت و منفی می‌شناسیم. همچنین دو بار نقطه‌ای نیروهایی بر یکدیگر اعمال می‌کنند که بزرگی این نیروها با مربع فاصله بین دو بار نسبت عکس و با حاصل‌ضرب اندازه بارها نسبت مستقیم دارد. این نیرو برای بارهای همنام دافعه و در مورد بارهای غیرهمنام جاذبه است (نیروی کولن).

آنچه گفته شد به افتخار شارل آرگوستن کولن (Chorles Augustim Coulumb) که از پیشروان الکتریسیته در قرن هیجدهم بود، به نام قانون کولن معروف است.

ترازوی پیچشی کولن

کولن دستگاهی ساخت که به وسیله آن می‌توانست نیرویی را که دو ذره باردار بر یکدیگر وارد می‌کنند، اندازه بگیرد. در ترازوی کولن میله‌ای دمبل مانند قرار دارد که به دو انتهای آن کره‌های کوچکی متصل شده است. این دمبل بوسیله یک رشته که از وسط دمبل می‌گذرد، آویخته شده است. هر گاه کره باردار دیگری را به یکی از کره‌های دمبل که قبلا باردار شده است، نزدیک کنیم، بر اساس قانون کولن با توجه به نوع بارها ، این دو یکدیگر را جذب یا دفع می‌کنند، بنابراین در اثر این نیرو دمبل خواهد چرخید و رشته تاب می‌خورد. با اندازه گیری زاویه انحراف دمبل می‌توان نیروی میان دو بار الکتریکی را سنجید. کاوندیش بعدها با الهام از ترازوی پیچشی کولن وسیله‌ای ساخت که برای اندازه گیری نیروی جاذبه گرانش بکار می‌رود (ترازوی کاوندیش).

به این ترتیب قانون کولن به صورت تجربی مورد تائید واقع شد. البته لازم به ذکر است که باور ما در مورد قانون کولن ، از نظر کمی مبتنی بر تجربه‌های کولن نیست. دقت اندازه گیریهای ترازوی پیچشی کولن به زحمت از چند درصد تجاوز می‌کند. به عنوان مثال ، چنین اندازه گیریهایی نمی‌تواند ما را متقاعد سازد که در رابطه قانون کولن توان فاصله بارها از یکدیگر دقیق برابر 2 است.

گستره عمل قانون کولن

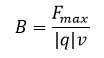
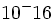قانون کولن در مورد بارهای نقطه‌ای بکار می‌رود. از لحاظ ماکروسکوپی بار نقطه‌ای باری است که ابعاد فضایی آن در مقایسه با هر طول دیگری در مسئله مورد نظر بسیار کوچک است. قانون کولن در مورد برهمکنش‌های ذرات بنیادی ، مانند پرتونها و الکترونها نیز صادق است. در مورد دفع الکترواستاتیکی میان هسته‌ها در فواصل بیشتر از نیز این قانون صدق می‌کند، اما در فواصل کمتر نیروهای پر قدرت و کوتاه‌برد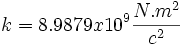 هسته‌ای عمل می‌کنند.

مشخصات قانون کولن

نیرویی که قانون کولن بیان می‌کند، به نیروی کولن معروف است. نیروی کولن بسته به نوع بارهای الکتریکی می‌تواند جاذبه یا دافعه باشد. قانون کولن یک قانون تجربی است، ولی با وجود این شواهد تجربی و نظری هر دو نشان می‌دهند که قانون عکس مجذور فاصله‌ای کولن دقیق است. آنچه قانون کولن بیان می‌کند، یک رابطه تناسبی است. با ضرب کردن طرف دوم در یک ثابت تناسب این رابطه تناسبی به یک تساوی تبدیل می‌شود. مقدار ثابت تناسب بستگی به دستگاه یکایی دارد که مورد استفاده قرار می‌گیرد.

به عنوان مثال ، در سیستم یکای گاوسی این مقدار ثابت را برابر یک فرض می‌کنند و یکای بار الکتریکی را به گونه‌ای انتخاب می‌کنند که رابطه با تجربه سازگار باشد. اما دستگاه SI که بار الکتریکی را بر حسب کولن ، فاصله را بر حسب متر و نیرو را بر حسب نیوتن بیان می‌کنند، ثابت تناسب باید کمیتی باشد که دارای بعد است. بوسیله آزمایشهای تجربی مقدار این ثابت تناسب بصورت زیر محاسبه می‌شود:
 

در بعضی از موارد به منظور ساده‌تر کردن محاسبه به جای مقدار فوق عبارت به ظاهر پیچیده را قرار می‌دهند که در آن 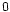کمیتی است که به عنوان ضریب گذردهی الکتریکی خلا معروف است و مقدار عددی آن برابر است.

برای حل مثال و تمرین از قانون کولن کلیک کنید.

اهمیت قانون کولن

مفهوم قانون کولن فراتر از توصیف نیروهای میان کره‌های باردار است. این قانون می‌تواند در فیزیک کوانتومی نیروهای الکتریکی که الکترونهای یک اتم را به هسته آن پیوند می‌دهد، نیروهایی که اتمها را به هم پیوند می‌دهند تا مولکول تشکیل شود و نیروهایی که برای تشکیل جامدات ، مایعات ، اتمها یا مولکولها را به هم پیوند می‌دهند، را به درستی توصیف کند. از این رو بیشتر نیروهایی که در زندگی روزمره خود با آنها سر و کار داریم، گرانشی نیستند، بلکه الکتریکی هستند.

در هسته اتم نیروی جدیدی وجود دارد که نه دارای ماهیت گرانشی است و نه الکتریکی. این نیروی جاذبه قوی که پروتونها و نوترونهای تشکیل دهنده هسته را به هم پیوند می‌دهد، نیروی هسته‌ای یا برهمکنش قوی هسته‌ای نام دارد. اگر این نیرو وجود نداشت، هسته در اثر نیروی دافعه کولنی قوی میان پروتونهای آن به یکباره متلاشی می‌شد.

منبع: دانشنامه رشد

دانلود حل المسائل فیزیک پایه یازدهم رشته ریاضی و تجربی

حل تمرین کامل فیزیک 2 پایه یازدهم تجربی و ریاضی دوره دوم متوسطه توسط کار گروه کتاب فیزیک پایه یازدهم در 148 صفحه و با پاسخ تشریحی برای کلیه فصول این کتاب تدوین شده است. برای دانلود حل المسائل فیزیک پایه یازدهم تجربی و ریاضی به ادامه مطلب بروید.حل المسائل کامل فیزیک 2 پایه یازدهم تجربی و ریاضی  برای تعامل موثر و سازنده با کتاب درسی و افزایش کیفیت یادگیری برای دانش آموزان گرامی  آماده گردیده است.این حل المسائل شامل پاسخ تشریحی کلیه فصول کتاب درسی است که شامل مباحث زیر می باشد :

( فیزیک 2 رشته ریاضی چهار فصل و رشته تجربی 3 فصل اول فیزیک 2 رشته ریاضی می باشد )

فصل اول : الکتریسیته ساکن 

1ــ1 بار الکتریکی 
1ــ2 پایستگی و کوانتیده بودن بار الکتریکی
1ــ3 قانون کولن 
1ــ4 میدان الکتریکی
 1ــ5 میدان الکتریکی حاصل از یک ذره باردار
1ــ6 خطوط میدان الکتریکی
1ــ7 انرژی پتانسیل الکتریکی 
1ــ 8 پتانسیل الکتریکی 
1ــ9 میدان الکتریکی در داخل رساناها 
1ــ10 خازن 
1ــ11 خازن با دی الکتریک 
1ــ12 انرژی خازن

فصل دوم : جریان الکتریکی و مدارهای جریان مستقیم  

2ــ١ جریان الکتریکی
2ــ2 مقاومت الکتریکی و قانون اهم 
2ــ3 عوامل مؤثر بر مقاومت الکتریکی
ٔ 2ــ4 نیروی محرکه الکتریکی و مدارها
2ــ5 توان در مدارهای الکتریکی 
2ــ6 ترکیب مقاومتها

فصل سوم : مغناطیس

3ــ 1 مغناطیس و قطب های مغناطیسی
3ــ2 میدان مغناطیسی 
ٔ3ــ3 نیروی مغناطیسی وارد برذره باردار متحرک در میدان مغناطیسى
3ــ4 نیروی مغناطیسی وارد بر سیم حامل جریان 
3ــ 5 میدان مغناطیسی حاصل از جریان الکتریکی
3ــ6 ویژگیهای مغناطیسی مواد

فصل چهارم : القای الکترومغناطیسی و جریان متناوب(رشته ریاضی)

4ــ1 پدیده القای الکترومغناطیسی
4ــ2 قانون القای الکترومغناطیسی فاراده
4ــ3 قانون لنز
4ــ4 القاگرها
4ــ5 جریان متناوب 

در فیزیک، درک واقعی یک مفهوم یا اصل، با توانایی در به کار بردن آن اصل در مسئله های مختلف مرتبط است. فراگیری چگونگی حل مسئله ها اهمیت اساسی دارد، شما فیزیک را خوب فرا نمی گیرید مگر آنکه بتوانید آنچه را فرا گرفته اید درموقعیتهای مناسب به کار برید.برای حل انواع مختلف مسئله های فیزیک به روشهای متفاوتی نیازداریم. صرف نظر ازنوع مسئله ای که در دست دارید، گامهای کلیدی مؤثری وجود دارندکه بایدآنها را مراعات کنید.مهمترین آنها تسلط کافی به مفاهیم کتاب درسی می باشد و مرحله بعد استفاده از جزوات حل تمرین در کنار کتاب درسی که به تسلط و تعمیق یادگیری دانش آموزان کمک بسزایی می نماید و قدرت تحلیل و حل مسائل را افزایش می دهد با استفاده از این جزوه حل المسائل دانش اموزان گرامی می توانند به این دو گام مهم دست بیابند و باعث افزایش راندمان و کیفیت یادگیری خویش در درس فیزیک شوند.

دانلود

کتاب فیزیک یازدهم ریاضی

دانلود کتاب فیزیک یازدهم رشته ریاضی و فیزیک

سر فصل های کتاب فیزیک یازدهم (سال دوم متوسطه دوم ) رشته ریاضی و فیزیک به شرح زیر است که با کلیک کردن روی هر کدام از آنها به جزوه های ریز مباحث هر فصل دسترسی خواهید داشت که علاوه بر بسط مطالب کتاب، از مثال ها و تمرین های بسیار متنوع استفاده نموده ایم و همچنین فایل های آموزشی از قبیل تصاویر و ویدیوها برای درک بهتر مفاهیم فیزیکی در هر مطلب قرار داده شده است.

فصل اول : الکتریسیته ساکن

فصل دوم : جریان الکتریکی و مدارهای جریان مستقیم

فصل سوم : مغناطیس

فصل چهارم : القای الکترومغناطیسی و جریان متناوب

کتاب تا سال تحصیلی ۹۸-۹۹ تغییری نکرده است.

دانلود کتاب فیزیک یازدهم ریاضی و فیزیک :

کتاب فیزیک یازدهم مخصوص رشته ریاضی و فیزیک

 

منبع: فیزیکفا

کتاب فیزیک یازدهم تجربی

دانلود کتاب فیزیک یازدهم تجربی

سر فصل های کتاب فیزیک یازدهم (سال دوم متوسطه دوم ) رشته علوم تجربی به شرح زیر است که با کلیک کردن روی هر کدام از آنها به جزوه های ریز مباحث هر فصل دسترسی خواهید داشت که علاوه بر بسط مطالب کتاب، از مثال ها و تمرین های بسیار متنوع استفاده نموده ایم و همچنین فایل های آموزشی از قبیل تصاویر و ویدیوها برای درک بهتر مفاهیم فیزیکی در هر مطلب قرار داده شده است.

فصل اول : الکتریسیته ساکن

فصل دوم : جریان الکتریکی و مدارهای جریان مستقیم

فصل سوم : مغناطیس و  القای الکترومغناطیسی

کتاب تا سال تحصیلی ۹۸-۹۹ تغییری نکرده است.

دانلود کتاب فیزیک یازدهم رشته علوم تجربی :

دانلود کتاب فیزیک یازدهم مخصوص رشته علوم تجربی

 

منبع : فیزیکفا